last section:

Horn-SAT is PTime-complete
SAT is NPTime-complete. by Cook’s
st-Con is NLogSpace-complete.
The problem QBF is PSpace-complete.
LP-feasibility is in PTime.
ILP is NPTime-hard. BEC 3-SAT ≤ log m ILP.
HAMILTONIAN-circuit is NPTime-complete

We can forget the ‘reasonably large’ non-deterministic space
classes.
LogSpace ⊆ NLogSpace ⊆ PTime ⊆ NPTime ⊆
PSpace ⊆ NPSpace ⊆ ExpTime ⊆ NExpTime ⊆
ExpSpace ⊆ NExpSpace ⊆ 2-ExpTime · · ·

• Savitch’s theorem simplifies this to:
LogSpace ⊆ NLogSpace ⊆ PTime ⊆ NPTime ⊆
PSpace ⊆ ExpTime ⊆ NExpTime ⊆
ExpSpace ⊆ 2-ExpTime · · ·

deterministic classes (time or space) are always equal to their
complement classes;
non-deterministic space classes from NPSpace upwards are
equal to their deterministic variants (Savitch) and hence to
their complement classes;
NLogSpace is equal to its complement class
(Immerman-Szelepcse´nyi).

LP

Diophantine : A equation in which all coefficients are integers and solutions
are sought over the non-negative integers is called
A system of linear equations
Ax = 0
is called homogeneous . The solution x = 0 is the trivial
solution .

Farkas’ Lemma

一定满足其中一个，不能两个都满足

There exists a vector x such that Ax ≥ b and x ≥ 0
There exists a vector y such that yA ≤ 0 and yb < 0

final final review

3-colourability

3个gadget

第一个是四边形，其中一个对角线连线，另外一组对角必须是不同颜色。
三角形一个点上面有一个点，上面这个点与三角形另外两个点必须有一个相同颜色。
两个三角形，两个点相连，然后另外两个点相连一个额外的点。这个额外的点与三角形的剩下两点需要不同颜色。
3的条件下其中一个点下面还有两个点，把这个有两个额外节点的点拿掉，这四个点中a一定有与bcd相同的颜色。

背下来吧还是:{(¬p1 ∨ ¬p2 ∨ p3),(¬p2 ∨ p4 ∨ p1),(¬p1 ∨ ¬p3 ∨ p2)}

Hamiltonian circuits

NPTime-Complete，从DHAMILTONIAN-circuit reduce 来的。
穿过所有的edge每个一次叫做Eulerian，穿过所有的vertex每个一次叫做Hamiltonian。
Eulerian: every node has even degree. LogSpace , PTime.

TSP

TSP feasibility：NPTime-complete

Matching (bipartite graph G perfect matching)

PTime , if 3D , NPTime-complete

SAT

reduce:

SAT -> k-SAT:

l1 ∨ l2· · · ∨ lm 可以转化成

p ∨ 3 ∨ · · · ∨ m
¬p ∨ l1 ∨ l2

不断重复上诉过程直到所有clauses最多只有三个元素。用LogSpace和PTime,所以说SAT比3-SAT简单。
SAT ≤log m 3-SAT

closed: many-one reduction 之后时间复杂度不变 Time(n),Time(n^2) 不是closed，sensible都是closed。
Commonly-encountered (i.e. sensible) complexity classes: 合理时间或资源的问题。P, NP, NP-complete, and NP-hard

many-one reduction:

P1 is (many-one polytime) reducible to P2 , 函数p1中所有的解都属于p2
P1 ≤p m P2

complete:

SAT is NPTime-complete. Horn-SAT is PTime-complete. st-CON is NLogSpace-complete. QBF is PSpace-complete.

final review

图论

strongly connected components

incident : 一条edge与旁边的两个vertex的关系就是incident。
in-degree : 指向这个vertex的edge数量。 out-degree 相反。
strong connected : 每一个vertex 都可以从其他vertex到达。
st-CON : 从一个点reachable到另外一个。DFS来算。
acyclic : 无环。如果是acyclic directed graph，存在vertex是zero in-degree。
SSCs : Strongly connected components

topological sorting

把所有的vertex的in-degree算出来。
从in-degree = 0开始，推到一个Stack里。
从Stack里面一个个抽出元素，放到res里面。
res调转顺序。
当一个vertex从Stack中弹出时，它的所有父节点都必须已经弹出，并且有一个较低的index。
如果all vertex都有index。就是拓扑排序。
如果不是，则G是cyclic，并且所有vertex都是non-zero in-degree。

RUNING Time: O(V + E)

strongly connected components

Kosaraju algorithm: O(V+E)

DFS, 记录DFS的顺序。
反转所有边。DFS，按到时间顺序的反转来访问。访问到的节点构成了SSCs。

Tarjan’s algorithm: O(V+E)

时间戳dfn: 每个vertex被访问的顺序。
追溯值low: 每个vertex的追溯值就是这个vertex的子树能到达的最小时间戳。
当当前追溯值等于时间戳，意味着这个带你是个强联通量的头节点，需要弹出。剩下的就是SSCs。

union find

connected components: linear time 可以找到
partition: 把graph分割成几个部分，每一个部分叫做一个cell
union-find(G) : O(E+VlogV)

makeSet

v.parents() = v
v.length() = 1
reutrn

union

把两个set连起来

Lemma

In a series of operations of makeSet, union and find on n
elements using the size-heuristic, no element can have its cell
field assigned more than blog nc + 1 times.
Proof.

Whenever v →cell changes, the cardinality of v → cell at least
doubles. But 1 ≤ |v → cell| ≤ n. This can happen no more than
blog nc times.
=== 1.30 ===

Lemma 2

With the above implementation, the running time of
union-find(G) is O(m + n log n), where n = |V| and m = |E|.

The total number of calls to makeSet, union and find is linear in
m + n. Each call involves a constant amount of work, apart from
updating v →cell. But each of the n vertices can have its
cell-pointer updated in this way at most blog nc times, yielding
total work O(m + n + n log n) = O(m + n log n).

fast and slow

Grzegorczyk hierarchy

Grzegorczyk层级是一个可数的层级，根据其计算复杂性，图灵机可以计算的函数。层次结构的每一级都被定义为可以通过Grzegorczyk还原法还原到上一级的函数类。

Γ0是原始递归函数类。这些函数可以由图灵机在有限的时间内计算出来。

Γ1 是原始递归有界函数类。这些函数可以由图灵机在有限的时间内用有限的资源量进行计算。如果存在一个原始递归函数g(n)和一台图灵机M，使得对于任何输入x，M最多经过g(|x|)步就会停止，并返回f(x)的值，则函数f(n)属于Γ1。

Γ2是递归有界函数的类别。这些函数可以由图灵机在有限的时间内计算出来，使用的是一个不一定是原始递归的边界函数。如果一个函数可以由图灵机使用某种可由图灵机计算的边界函数来计算，那么它就属于Γ2。

Γ3是可递归列举的函数类。这些是可以被图灵机部分计算的函数。如果一个函数可以被图灵机计算，但对于给定的输入不一定会停止，则该函数属于Γ3。

Γ4 是一般递归函数类。这些是可以由图灵机计算的函数。如果一个函数是可以由图灵机计算的，那么它就属于Γ4。

值得一提的是，Γ0是Γ1的适当子类，Γ1是Γ2的适当子类，Γ2是Γ3的适当子类，Γ3是Γ4的适当子类。层次结构中的每一级都严格包含在下一级中。

exponentially bounded

doubly exponentially bounded

k-tuply exponentially bounded

flow networks and matching

max flow : flow的最优解

The Ford-Fulkerson algorithm

N = = (V,E,s,t,c) : (V,E)是一个graph,s和t是起始和终点,c是赋值。

bipartite graph

G = (U,V,E) where U and V are disjoint, E 属于 U x V

perfect match : 左右两边的节点一对一全对上

maximum matching : matching 有着最多数量的edges。

naiveMatch : 寻找matching，不断递归，删除左边和右边一个点，和他们之间的边。到最后判断是否两个集合都是空，是的话Yes，否的话No。

Busacker-Gowen algorith

minmimum cost and max value

begin flowMaxCost(V,E,s,t,c,γ) set f (e) = 0 for all e ∈ E
while
reachable(Nf ,s,t)
let e1,…,em be the edges on a shortest path from s to t for 1 ≤ i ≤ m
ifei ∈E,incrementf(ei)
else decrement f (e−1) i
return f

String

The Boyer-Moore Algorithm : 相比于暴力遍解，只需要加两个启发式。

Looking-Glass Heuristic: 当第一个字节匹配，我们也同时检测最后一个substring是否匹配。

Character-Jump Heuristic: 如果string中有一个字符substring都不存在，直接跳到这个字符串后面。

Knuth-Morris-Pratt Algorithm : 有一个判断子字符串的重叠信息，比如abcabcd 就是 0001230 这个叫做 $\pi$

图灵机

machine stops

time,space and determinism

CO-NLogSpace: cannot solved by non-deterministic algorithms
Davis-Putnam algorithm : 目的是验证satisfiable

try to be logical

Horn: 一个clause最多只能有一个positive的literal，就是Horn。并且都是vvvv这种形式的。所以能从VVVV -> (and and and)-> 正的那个元素
Horn set: PTime 因为它可以用一种叫做Chandon和Lewis算法的线性时间算法来解决。这个算法的工作原理是：首先将Horn公式转换为等价的共轭正常形式（CNF）公式，然后使用深度优先搜索来检查CNF公式中变量的满足性分配。由于CNF公式的大小与原始Horn公式的大小成多项式，因此该算法的总体时间复杂度也是多项式的。
Krom: 一个cluase最多只有俩元素。该算法首先将Krom公式转换为等价的共轭正常形式（CNF）公式，然后使用深度优先搜索来检查CNF公式中变量的满足性分配。由于CNF公式的大小与原始Krom公式的大小成多项式，因此该算法的总体时间复杂度也是多项式的。
QBF : 加上存在和所有。Pspace。因为画个二叉树就行了。
QBF sentence : A quantified Boolean formula with no free variables is called a
quantified Boolean sentence.

how hard can this be

many-one reduction 就是一个问题a比另外一个问题b更加复杂，也就是说如果能解决困难的问题a，也就可以使用它去解决简单的问题b。many-one就是将许多的输出映射到一个函数。

为了证明一个问题可以many one reduction 到另一个问题，你需要定义一个函数，该函数接收第一个问题的输入并产生第二个问题的输出，这样，只要第一个问题的输入是第一个问题的有效输入，第二个问题的输出就是第二个问题的有效解。这个函数被称为从第一个问题到第二个问题的多一还原

多一还原经常被用来证明一个问题是NP-hard的，这意味着它至少和NP中最难的问题一样难。如果一个问题是NP-hard，那么它就被认为是非常难解决的，而且不太可能找到一个有效的算法来解决它。

closed : many-one reduction 之后时间复杂度不变

Two NP-Complete problems

凸优化

Integer Linear Programming

Two Theorems on Space Complexity

Savitch’s theorem

Week 4

Turing Machines (我自己的理解)

palindrome问题

我们可以用one tape来实现判断回文。在这种情况之下，先看input的第一个，read（再这里是不用write的）head。然后在通过O(n)，n是字符串长，来跑到最后一位，判断是否相等。如果相等，继续，不想等，halt。直到判断完所有为止。

那么two tape呢。比如可以第一个tape从头往后，第二个tape从后往前，判断是否相等。

但是怎么样每一个tape在一半的时候停止呢？我们可以用一个counter来计算，图灵机在判断开始前知道了字符串长度，维护counter就可以了。这个counter并不需要额外的tape去实现。
如果我们有一个set的string怎么判断回文呢？我们可以把所有的set连起来，比如”level-after-halo”。也可以图灵机嵌套去图灵机，但是这样的话图灵机只能输出单一string了。
‘-‘该用在哪里呢？可以用在判断字符串结束比如one tape中的input是”level-“.

binary reverse问题

每一次读取需要给1变成0，0变成1，这就涉及到了read/write head 同时使用的地方了。

并且还有一个点就是read/write 是隶属于head的功能，head移动，可以做read/write这两个事，认清从属关系。

Turing Machines

控制单元K，读取一个特殊的sequence of symbols 在 K tapes 上。

T : control unit （finite set of unstructions）
Tapes : 除了第一个(input) 和最后一个(output) tape, 别的都是working tape
read/write : 小横杠，读取
Q : 可以简单的理解为
state : 一行数字，10101010110 (老师这么说但貌似不是这样，state是end ，start这些东西)

transition

如果当前state是p，reading sequence s，移动到state q，write sequence t，direction d.把一个configuration变成另外一个configuration

configuration

head 在哪，你也知道turing machine 是啥。It’s a current memory dump of the turing machine.每一个tape都是什么状态的。

run

Handy notation

x 就是从alphabate 里面选取的一个string

每一次turing machine 都开始于 blank , 然后过一段时间，没有avaiable transitions，the run stop。

我们假设有avaiable transitions， run就不会stop。

$M\downarrow x$ given input x, all of the types is blank except the input,之后会停止

$M\uparrow x$ 有可能会停止，有可能一直运行

在我的看来就是这个M会在input为x的时候停止或者停止不了。

用single number来表示图灵机

transition is a turple

transition table is a sequence of tuple.

图灵机里的啥都是turple，所以我们可以用single number来表示。问题的关键在于。

可以把一个图灵机当作input放入另外一个图灵机。

acceptance and recognition

如果一台图灵机在给定输入时停在一个接受状态，那么它就被称为 “接受 “输入。接受状态是一种特殊的状态，它被指定为机器可以停止的地方，并且仍然被认为是成功完成了它的任务。这通常用于表明输入是图灵机所要解决的问题的有效解决方案。

如果一台图灵机在给定输入时停在接受状态或拒绝状态，就可以说它 “识别 “了输入。拒绝状态是一种特殊的状态，它被指定为机器可以停止的地方，并被认为是未能找到解决方案。这通常用于表明输入不是图灵机所要解决的问题的有效解决方案。

因此，综上所述，”接受 “输入的图灵机是在给定输入时能够成功解决问题的机器，而 “识别 “输入的图灵机是能够确定输入是否是问题的有效解决方案的机器。

其他的一些零碎定义

If a language is recognized by some Turing machine M , then it is recognized by some determinisitc Turing Machine M’。我的理解是图灵机可以嵌套。
language 和（decision） problem的意思一样， recursive和decidable的意思一样

recursively enumerable (r.e.)

如果一个语言(language)是recursively enumable的，也就意味着存在一个图灵机，图灵机会enumerable（list）这个语言中所有的strings。重点是，他不需要有能力去算出给定的input string 在不在这个语言之中。

举个例子: {x ∈ {0, 1}∗ | x denotes a prime number}

x属于这个是二进制，比如3的话就是11. *是Kleene star，表示的是x可以是任何数字在里面。

recursively decidable language

recriively enumerable languages 是recursively decidable languages的subclass。他的意思就是图灵机能不能判定input的string在不在我们指定的language之中。图灵机可以在所有的input上停止。

problem

举例子:
Consider the problem of determining whether a formula of
propositional logic is satisfiable
p0 ∧ (p1 → p10)
¬((p0 ∧ p1) ∨ (p0 ∧ ¬p1) ∨ (¬p0 ∧ p1) ∨ (¬p0 ∧ ¬p1))
This problem is the language language
{x ∈ {p, 0, 1, ∧,(,), ∨, ¬, →}∗
| x is a wff and satisfiable}.

解释：
The language being considered is defined as the set of all strings x in {p, 0, 1, ∧,(,), ∨, ¬, →}^* (i.e., all finite strings of symbols from the alphabet {p, 0, 1, ∧,(,), ∨, ¬, →}) that represent a well-formed formula (wff) of propositional logic and are satisfiable.

In other words, this language consists of all strings that represent formulas of propositional logic that can be satisfied (made true) by assigning values to the propositional variables in such a way that the formula evaluates to true.

定义

problem name:
given : a string x (coding some object we are interested in);
return : Yes if x has some property P , and no otherwise.

Halting problem

HALTING
Given: a pair of strings m, x;
Return: Yes if m is the code of a deterministic Turing Machine, M, and x a string in the alphabet of M, such that M ↓ x;
No otherwise.

定义

The halting problem is a famous problem in computer science that asks whether it is possible to determine, given a description of a Turing machine and an input string, whether the Turing machine will halt (stop) when run on that input.

More formally, the halting problem can be stated as follows:

Given a Turing machine M and an input string x, is it possible to determine whether M will halt when run on x?

The halting problem is undecidable, meaning that there is no algorithm or procedure that can always correctly determine whether a given Turing machine will halt on a given input. This means that it is not possible to write a program that can determine, for any arbitrary Turing machine M and input string x, whether M will halt when run on x.

The halting problem is a fundamental result in computability theory and has important implications for the limitations of computability and the design of programming languages.

题目

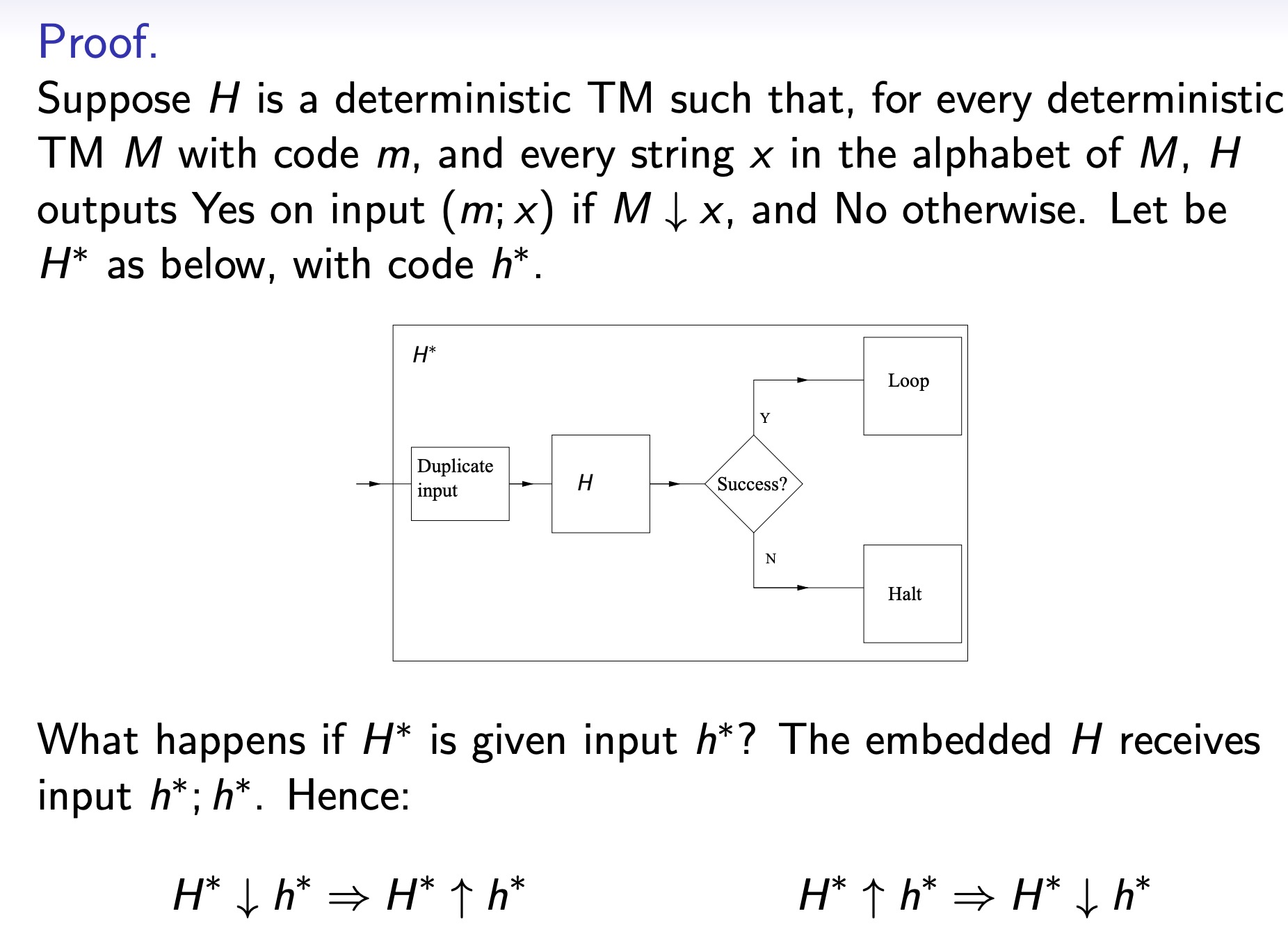
总结

In this lecture, we have:
• explained the origins of research into computability theory,
including Hilbert and Ackermann’s Entscheidungsproblem;
• defined Turing machines and the notion of a decidable problem
(= recursive language);
• proved the existence of undecidable problems, and indeed
answered Hilbert and Ackermann’s question in the negative.

week 7

Propositional logic satisifability

proposition letters : P = {p1,p2,p3} 元素符号
formulas : $\phi$ 公式
assignment : $\theta$ P -> {T,F} 赋值，例子：θ(¬ϕ1) = T iff ϕ1 = F
satisfiable : 存在一种assigmen 使得formula = Ture
proposition letters(variables): p&q 的p和q
connectives: &, v, ->, and <->.
leteral: p or ¬p (p is proposition letter)
opposite leteral : l 上面一个横杠
clauses : 每个formula都是一个clause，一堆公式就是clause

clause: A clause is an expression l1 v l2 v· · · ∨ k , where the li are
literals. ep: p1 ∨ ¬p2 ∨ p3

propositional SAT

Given: a propositional logic formula ϕ;
Return: Yes if ϕ is satisfiable, and No otherwise.

SAT
Given: a set of clauses Γ;
Return: Yes if Γ is satisfiable, and No otherwise.
k-SAT
Given: a set of clauses Γ, each with at most k literals;
Return: Yes if Γ is satisfiable, and No otherwise.

Davis-Putnam algorithm

目的是验证satisfiable

resolve : 移除但个元素

DPLL :

special cases

Horn

一个clause最多只能有一个positive的literal，就是Horn。并且都是vvvv这种形式的。

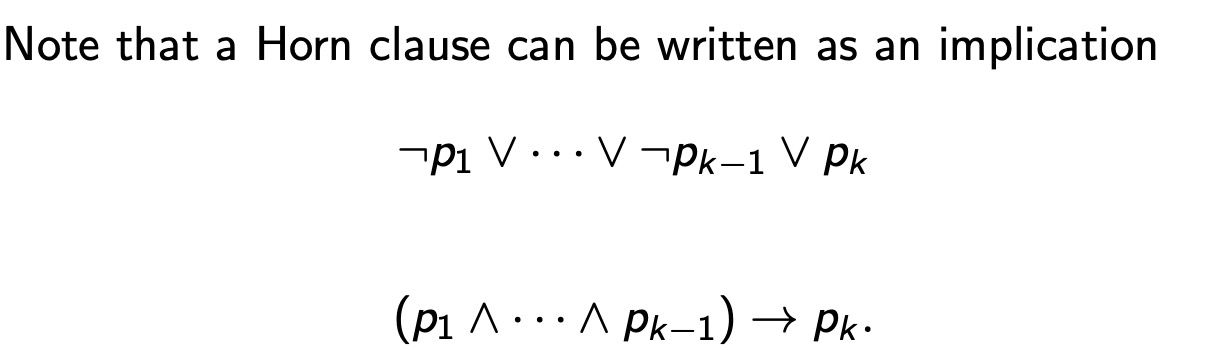
Horn-SAT

in PTime

Given : a set of Horn-clauses
Return : satisfiable or not

Krom

一个cluase最多只有俩元素。

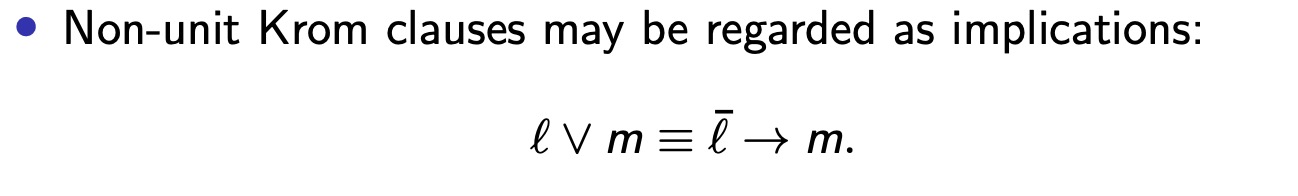
KROM_UNSAT

NLOGSPACE （由很多答案true或false来组成）

跳过: KROM_UNSAT 的证明

QBF (quantified boolean formula)

就是带上$\exists$ and $\forall$

在我看来就是描述相似的function的符号。

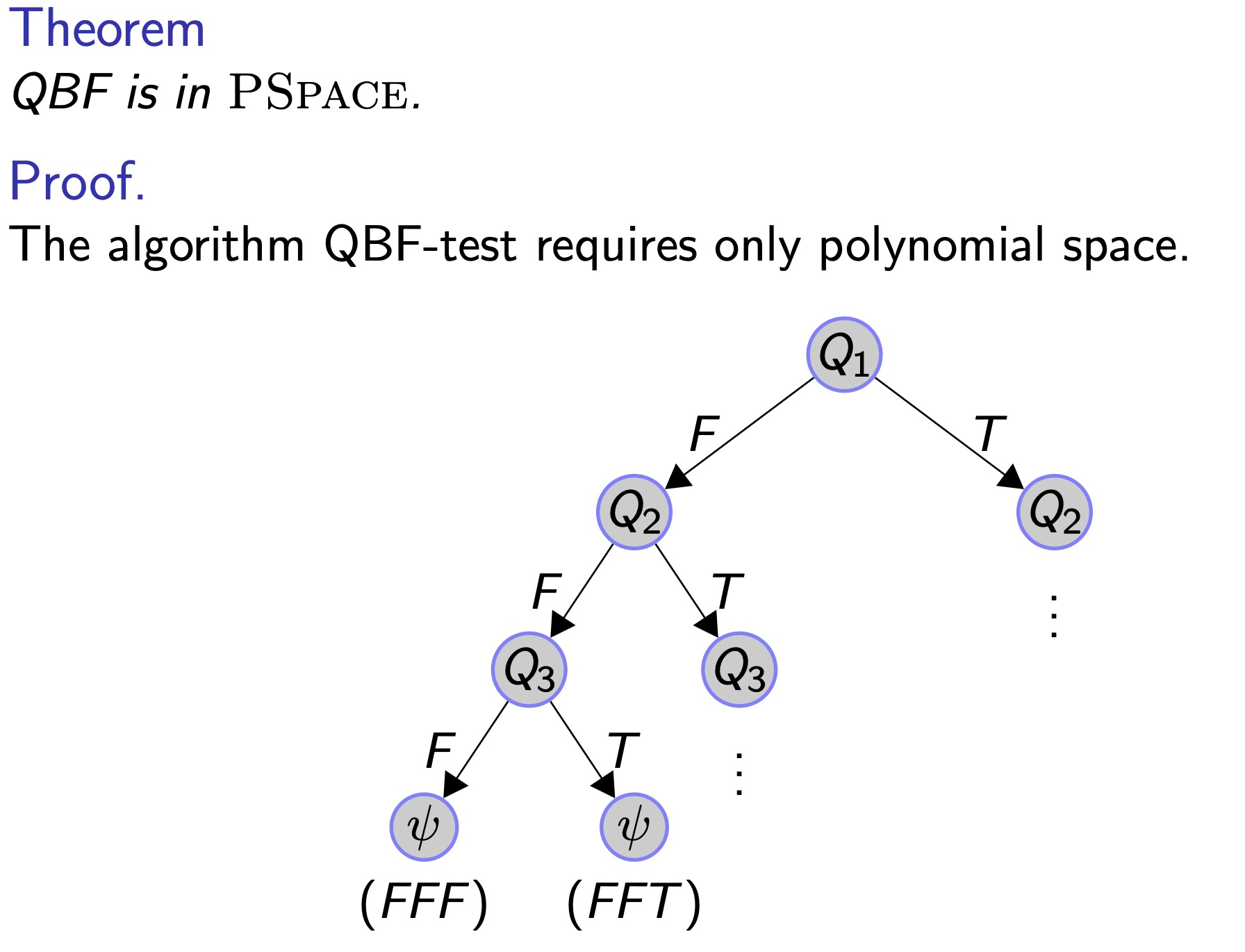
总结

Week 5

runs in time & space

g is a function that maps natural numbers (i.e., non-negative integers) to natural numbers. The expression g(|x|) refers to the value of the function g applied to the input |x|, where |x| is the length of the string x.

In other words, g(|x|) is the output of the function g when the length of the string x is used as the input. For example, if |x| = 5 and g(n) = n^2, then g(|x|) = g(5) = 5^2 = 25.

In the context of the definition you provided, g(|x|) represents the maximum number of steps that a Turing machine M is allowed to take when run on input x, where the number of steps is determined by the function g applied to the length of the input string x.

The definition states that M runs in time g if, for all but finitely many strings x in the alphabet Σ*, any run of M on input x halts within at most g(|x|) steps. In other words, M must halt within a number of steps that is determined by the function g applied to the length of the input string x, except for a finite number of strings x.

Time(g) and Space(g)

Let L be a language over some alphabet, and let g : N → N be a
function. We say that L is in Time(g) if there exists a
deterministic Turing machine M recognizing L such that M runs in
time g.

Let L be a language over some alphabet, and let g : N → N be a
function. We say that L is in Space(g) if there exists a
deterministic Turing machine M recognizing L such that M runs in
space g.

回文

文中说Time(3n+1) ， Space$(\upharpoonright logn \upharpoonleft)$。其实这里应该弄清楚了，时间复杂度是O(3n+1),是因为他课上讲的脑瘫方法所致，但空间复杂度可以通过这种方法达到O(logn):

先给input分成两个部分，比较前者和后者的inverse是否相同，如果相同，再给每一部分分成两个再进行比较。递归到一个个元素为止。

注意:The space complexity is determined by the number of memory units required to store the data needed by the algorithm as it is running.

speed-up

PTime = Time(P)
ExpTime = Time(E)
k-ExpTime = Time(Ek)
LogSpace = Space(log n)
PSpace = Space(P)
ExpSpace = Space(E)
k-ExpSpace = Space(Ek)

st-CON

一个有向图 G，有顶点u和v

return : v是否reachable from u, N otherwise

TSP feasibility

旅行商问题，绕所有的点不重复并且回到原点

k-COLOURABILITY

Given: A graph G.
Return: Yes if G is k-colourable, and No otherwise.

回到图灵机

Week 8

k-SAT

Given: A set of clauses $\Gamma$ each of which has at most k literals.
Return: Y if $\Gamma$ is satisfiable, and N otherwise.

我们现在有一个set of (proposition al logic) clauses。我们拿来一个新的proposition letter : p, 然后给他全都装进去。

之前是 l3v…vlm 和 l1vl2
现在是 pvl3…vlm 和 -pvl1vl2

reduction

我的理解

many one reduction 定义

P1 和 P2 分别对应字母表 $\Sigma1$ 和 $\Sigma2$

我们说P1(many-one logspace) reducible to P2，如果存在function可以做到字母表1映射到字母表2通过一个function(f),并满足以下两点:

function f 可以在deterministic 图灵机使用在一个最多为log n space的任何工作tape上。
对于$\Sigma1$里所有的x，x属于P1，iff，f(x)属于P2

closed

property of a complexity class remain under a many-one reductions.

Commonly-encountered (i.e. sensible) complexity classes

有些是close的有些不是。

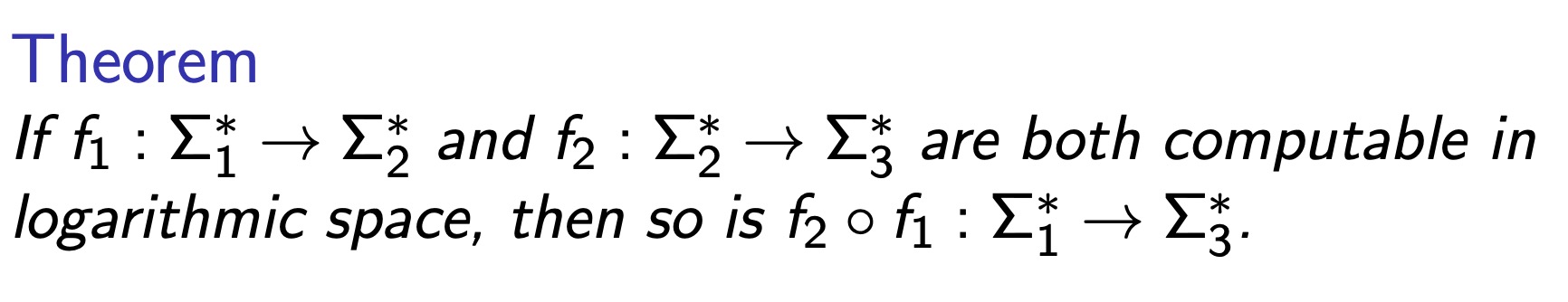
图示上公式。

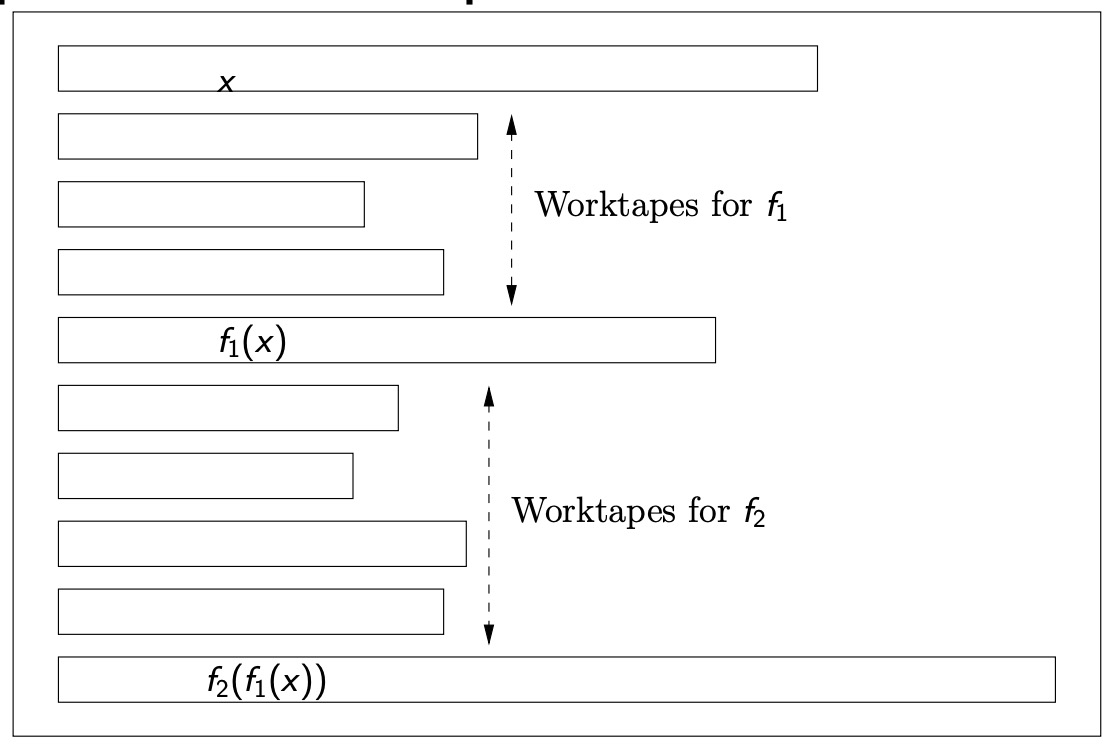
Calculate the first bit of f1(x).
Initialize a counter to 1 (to keep track of which output bit we are calculating).
Start a simulation of f2(f1(x)), using the calculated bit as input.
If the simulation of f2 asks to move the read head to the right:
1. Calculate the next bit of f1(x).
2. Write it on top of the current bit.
3. Update the output bit counter.
If the simulation of f2 asks to move the read head to the left:
1. Restart the calculation of f1(x).
Continue until the required output bit is calculated.
Write it on top of the current bit.
Update the output bit counter.

向左移动是因为他遇到了left end，”-“，啥的，让他结束进行下一个计算。

总结

Cook’s theorem

主旨

SAT is NPTime-complete

week 9

k-colourability

NPTime for all k

3-colorability is NPHard

Encoding of {(¬p1 ∨ ¬p2 ∨ p3),(¬p2 ∨ p4 ∨ p1),(¬p1 ∨ ¬p3 ∨ p2)}

Hamiltonian circuits

每一个vertex只走一次

HAMILTONIAN-circuit is NPTime-complete.

A cycle that travels exactly once over each edge in a graph is called “Eulerian.” A cycle that travels exactly once over each vertex in a graph is called “Hamiltonian.”

Eulerian circuit

if a graph has an Eulerian circuit, then every vertex must have an even degree, since the circuit visits every edge exactly once and each edge is incident to two vertices.

The problem EULERIAN-circuit is in LogSpace, hence certainly
in PTime.

week 10

Carathéodory’s theorem

如果你有一个n维空间中的点集，你可以找到最多n+1个点的凸组合（系数为非负且和为1的组合），其中包括该集凸壳中的任何其他点。

设E是一个由m个线性方程组成的系统。如果E有一个解在R+，那么它就最多只有m个entries是正的。
如果linear equations 在正实数集合上(R+)有一个解，那么它在正有理数集合上(Q+)也会有一个解（形式为a/b的数字，其中a和b是正整数）。解决方案中的有理数的分子和分母将被(2mM)^m所限制。

R+ : 非零正数

E : Ax = b , e is a solution over R+

LP(linear programming)

LP-feasibility is NPTime
LP-infeasibility is NPTime by Farkas’ Lemma
E : Ax = b

#36111

algorithm_review

http://example.com/2023/01/04/algorithm-review/

Author

Chenxi Qu

Licensed under

我的kpi Previous

grapic_review Next