算法-笔记2

fast and slow

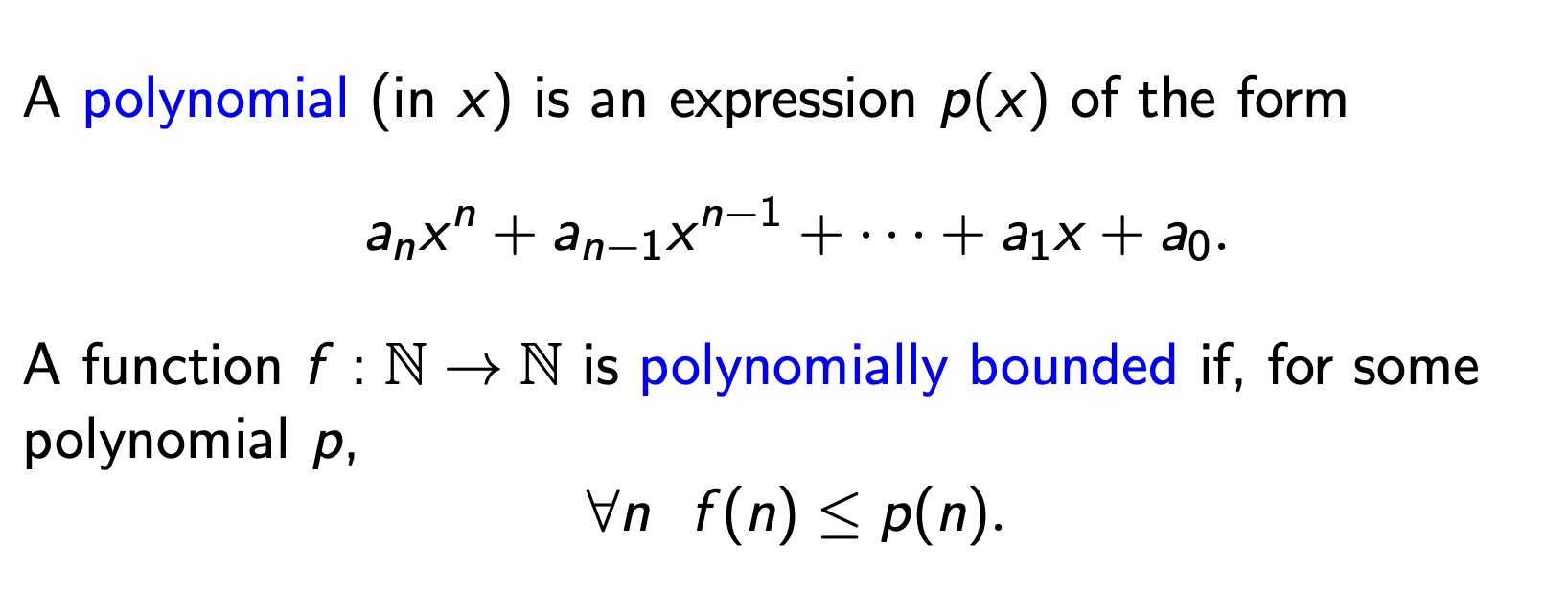
n! —> singly

• 2^n <= n <= 2^n^2

Ackermann Function

用来描述递归时间复杂度的方程。

k-fold就是在表示递归，下图描述的更加直观。

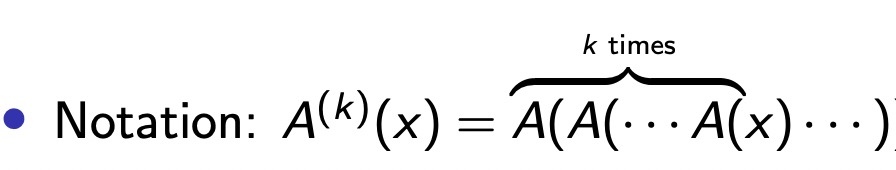
注意A3是大于等于，要推到A2才能算出精确值

上面的推导过程

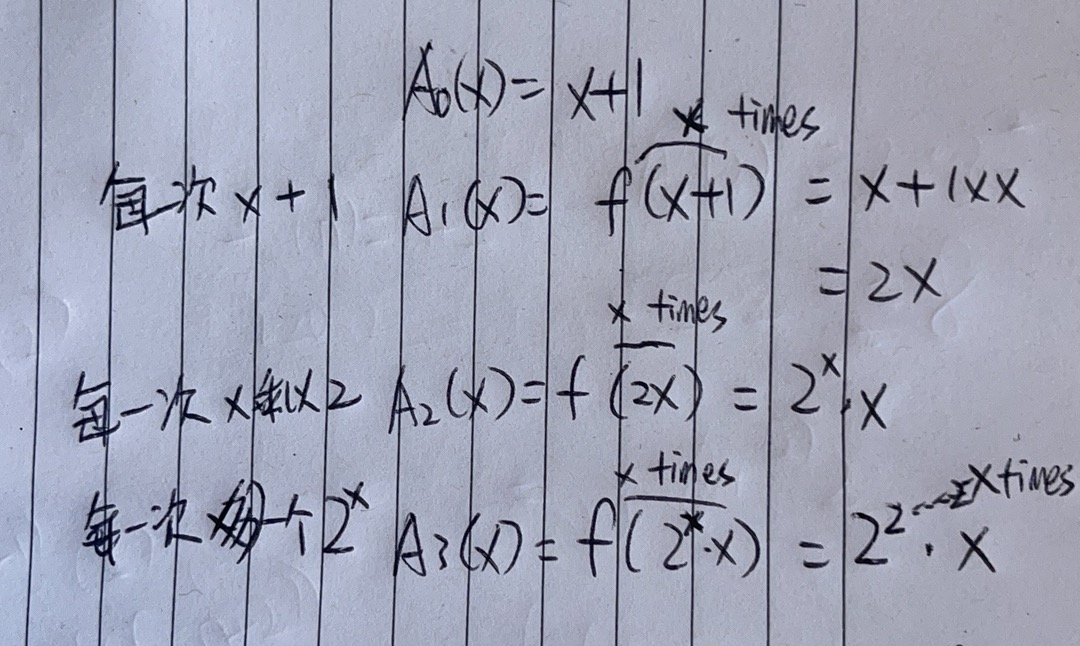
String

The Pattern Matching Problem

找子字符串

Example 23.1: Suppose we are given the text string
T = “abacaabaccabacabaabb”
and the pattern string P = “abacab”
Then P is a substring of T . Namely, P = T [10..15].

Σ : alphabet

Brute-Force Pattern Matching

暴力遍解 也叫 naive algorithm

Running time O(T*P)

T P 一个substring 一个 string

Rabin-Karp algorithm

先check substring的numbers 再check它是否匹配。

Worst-case Running time O(T*P)

O(n+m+m(n/q))

• q: modulo (always prime)

The Boyer-Moore Algorithm

相比于暴力遍解，只需要加两个启发式。

• Looking-Glass Heuristic: 当第一个字节匹配，我们也同时检测最后一个substring是否匹配。

• Character-Jump Heuristic: 如果string中有一个字符substring都不存在，直接跳到这个字符串后面。

Worst-Case Analysis of the Boyer-Moore Algorithm

The worst-case running time of the BM algorithm is O(nm + |Σ|). Namely, the computation of the last function takes time O(m + |Σ|) and the actual search for the pattern takes O(nm) time in the worst case, the same as the brute-force algorithm. An example of a text-pattern pair that achieves the worst case is

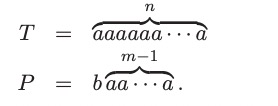
这个方法的shift不是很好。所以有下面方法。

Knuth-Morris-Pratt Algorithm

KMP 是线性复杂度。

longest prefix of the good prefix is also a proper suffix of the good prefix 。

增添回溯的Boyer-Moore Algorithm。不像之前一个个字符的判断。而类似于贪婪，检测substring和string的匹配关系直到遇到不匹配的字符。通过咨询失败函数来判断新的索引。

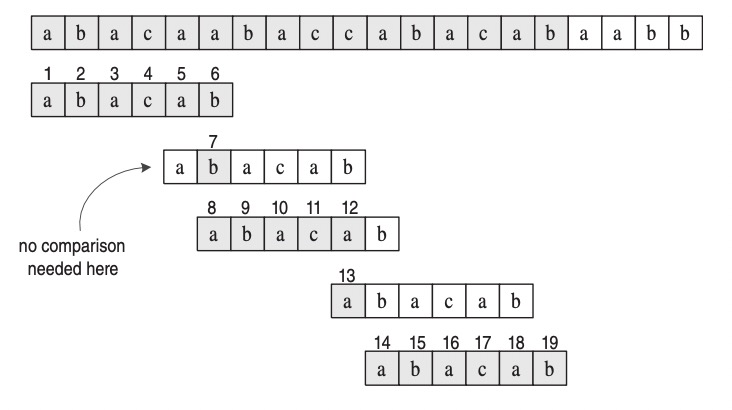
compute π：

Using a similar reasoning, the running time of compute-π(P)
is O(|P|).

begin naiveCompute-π(P)
π(0) ← 0
for i = 1 to |P| − 1
π(i) ← −1 
for i = 1 to |P| − 1
j ← 0
while i + j < |P| and P[i + j] = P[j]
if π(i + j) = −1
π(i + j) ← j + 1
if j = 0
π(i) ← 0
j ← j + 1

remove unnecessary shifts

better:

begin naiveCompute-π(P)
π(0) ← 0
for i = 1 to |P| − 1
π(i) ← −1
i ← 1
j ← 0
while i < |P|
while i + j < |P| and P[i + j] = P[j]
if π(i + j) = −1 // match
π(i + j) ← j + 1
j ← j + 1
if j > 0 // mismatch
i ← i + j − π(j); j ← π(j)  
else
π(i) ← 0; i ← i + 1

线性复杂度的原因是在循环之中不是 i 就是i+j increases。

The running time of KMP(T,P) (ignoring the construction of π is O(|T|).