modeling 笔记

line

polyline: 连续的折线

line: 不管啥样的线都是1D的。line 包含curve。

左边的公式适用于在曲线上生成点（为了pipeline）

右边的公式适用于描述trajectories(轨道)。可以用来延续一条curve。

define 1D curve in 3D space.

Speedline

curve上取两个及以上个数的点。

interpolation : curve经过了所有的specify points

approxmiation : curve没有必要经过所有的点

cubic bezier curves

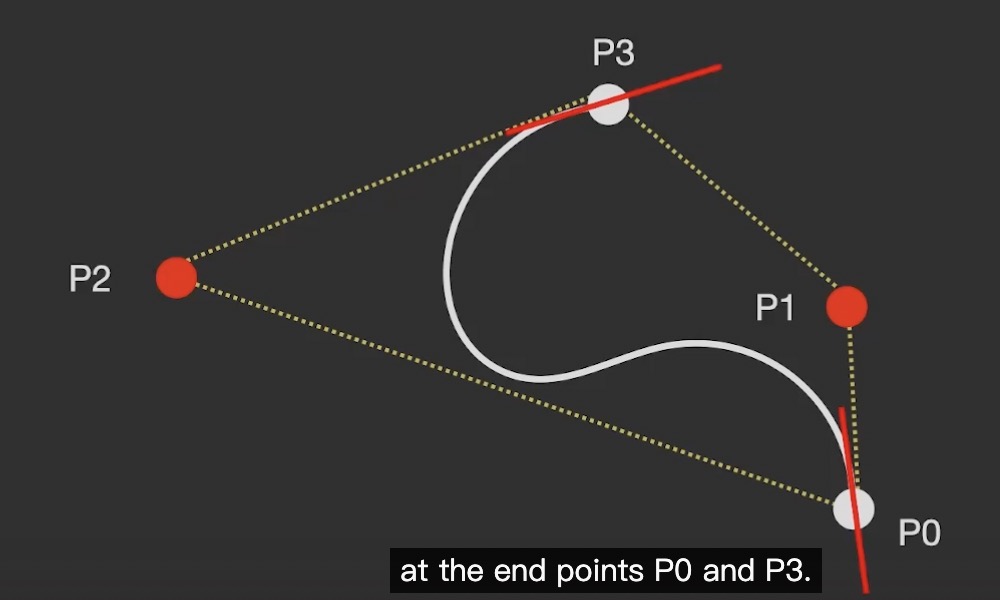
这种曲线总是被control points 组成的convex包裹着

注： 曲线在endpoint 正切

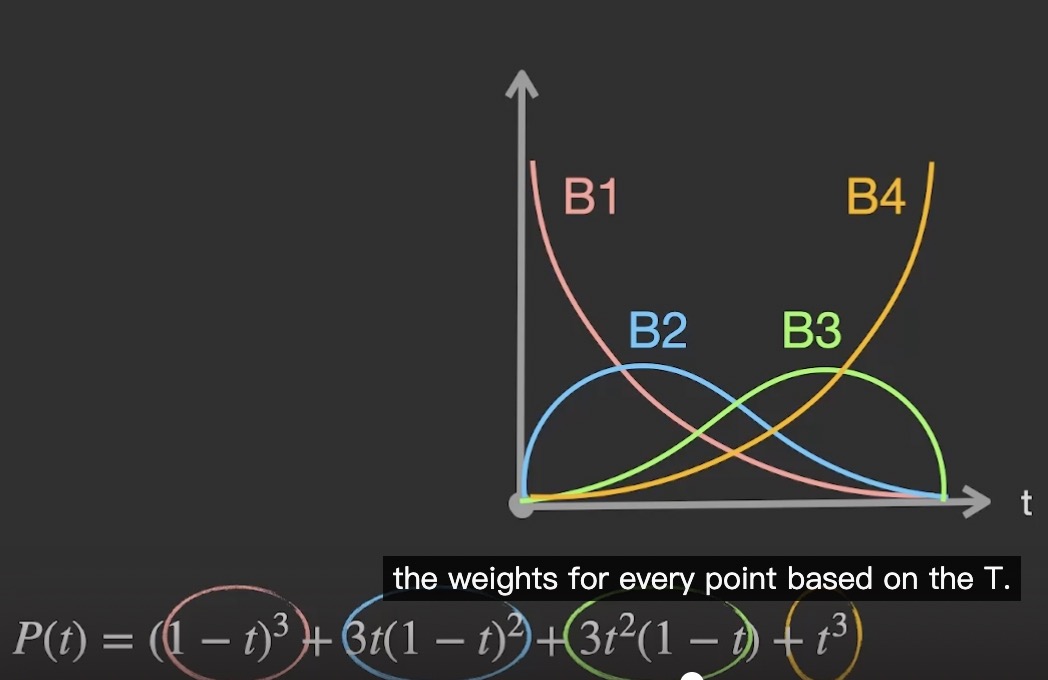
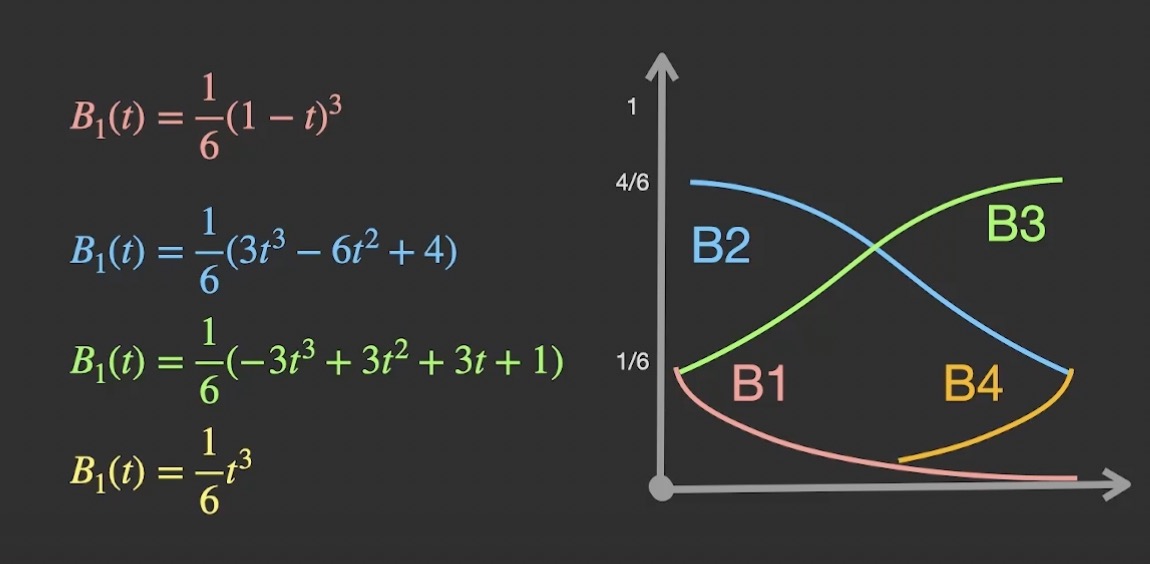
图像描述了每一个基于T的点的权重值

性质: partition of unity : 相加得1 ; T [0,1] . 所以被convew包裹着

matrix1： control points

matrix2: coefficient

matrix3: Bernstein polynomials

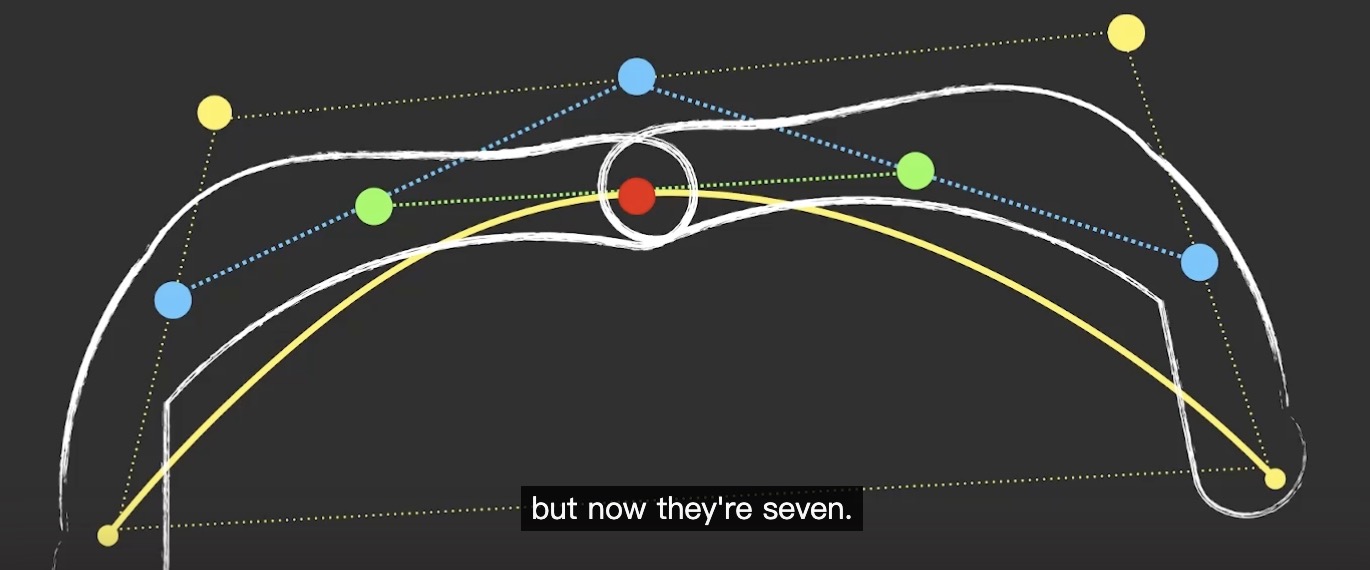
使曲线变得更复杂。如图采取中点。给曲线由3个control points 变成7 个。

注: 也可以不是中点 而是任意的radio。

continuity

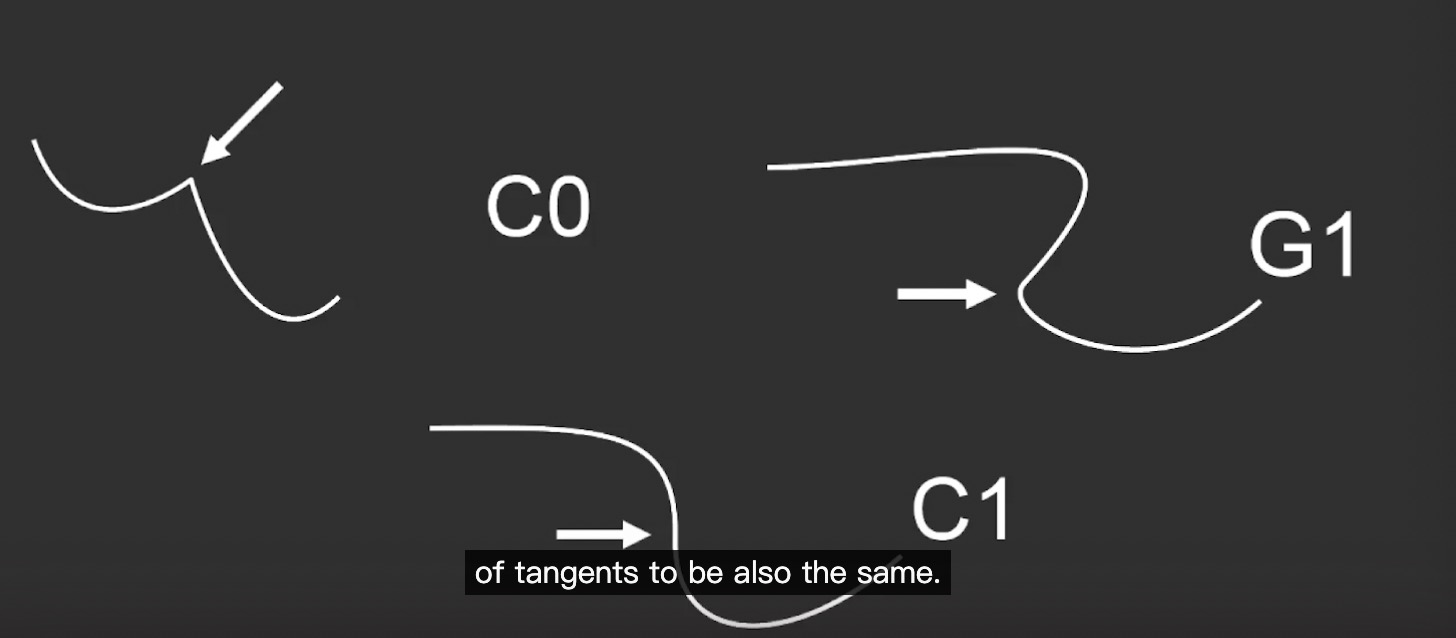
C0 : 两条curve相交点是sharp kink。

G1 : 两条curve相交点tan是同一个direction。

C1 : 两条curve相交点tan完全相同。

C2 : 两条curve相交点tan完全相同，导数也完全相同。

cubic BSP line

BSP vs Bezier

BSP 不经过endpoints

Bezier 经过

surface

给一个线拉成平面

Implicit surface

在数学中，隐式曲面是欧几里得空间中由方程定义 的曲面。
F(x,y,z)=0
隐式曲面是三个变量的函数的零点集合。隐式意味着方程没有求解x或y或z。

ep: 球体 x^2+y^2+z^2 = n^2

Parametric Surface

输出的成分是基于一些参数或参数的。

如二次贝塞尔曲线（其中A、B、C和CurvePoint是N个维度的点）。
CurvePoint = f(t) = A*(1-t)^2 + B2t(1-t) + Ct^2

或单位圆。
x = cos(t)
y = sin(t)

或者像这样的曲面。
SurfacePoint3D = f(u,v)

explicit surface

比较常见的函数类型，你在左边有一个变量（因变量），右边有另一个变量（自变量）。

比如说线。
y = mx + b

或高度场。
高度 = f(x,y)Ackermann Ackermann

L * R = C

The color gets less saturated as gets closer to white.