games101_笔记(光追)
intro :
因为光栅化(rasterization)没法做到很真实的物理效果,所以我们尝试使用光线追踪(ray tracing), 因为光追会显现出来更加真实的物理效果,反之会消耗更多的时间去渲染。
step 1 (light rays):
尽管光追能做到拟真是世界光源,但光线追踪和物理上光的反射不太一样,在cg中我们这么定义:
- 光沿直线传播
- 光线相交互不影响
- 光路可逆,光线传入眼睛可以当作眼睛发出光线。
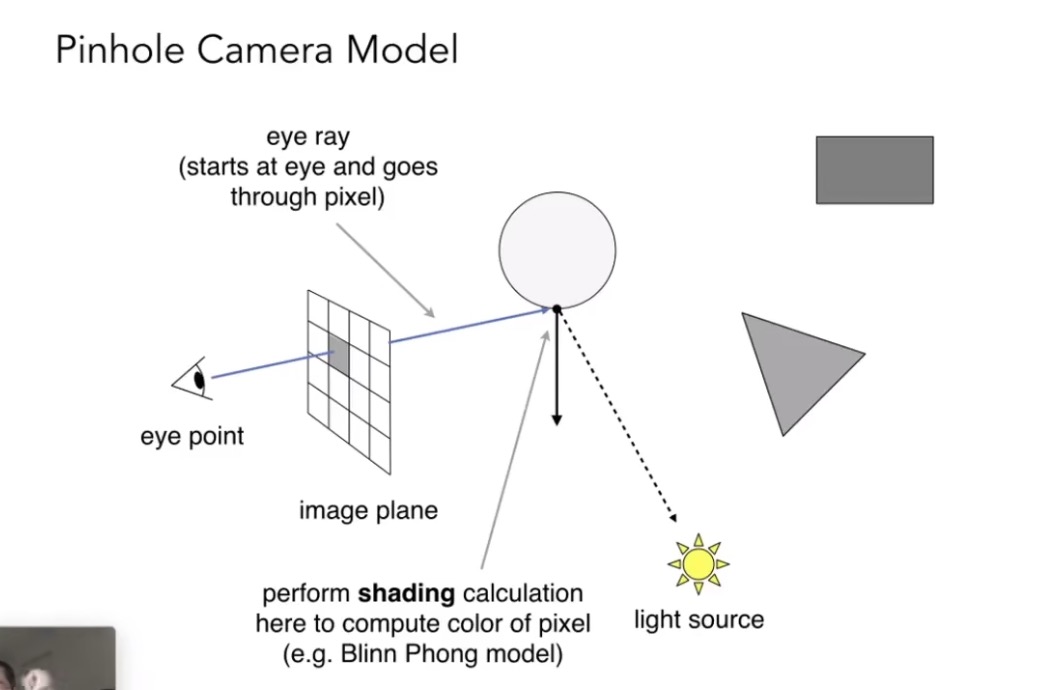
step 2(pinhole camera model):
每一个像素(pixel)投射一个光线,寻找这条光线所经过的路径,并判断与光源之间有没有被遮挡。如图所示,从light source返回一条光束,在之后通过镜面反射进入人眼。
但这个模型只有一次反射,和光栅化区别不大。于是whitted提出下面的模型。
step 3 (whitted-style):
就是将单一的pinhole camera model 进行递归 ,从而模拟出光线多次反射的效果 ,命名为recurive ray tracing 。但需要注意以下两点:
- 光线强度会随着反射次数的增加而逐渐衰减。
- 每个三角形的光都有可能是由很多个光源复合而成的。这里就涉及到了权重值问题,比如黄色光和红色光同时射入,这个三角形应该被渲染成橘色。但由于入射光的亮度可能不同,橘色的深浅也有不同。通过不断的累加颜色最终得到像素应该呈现的颜色。
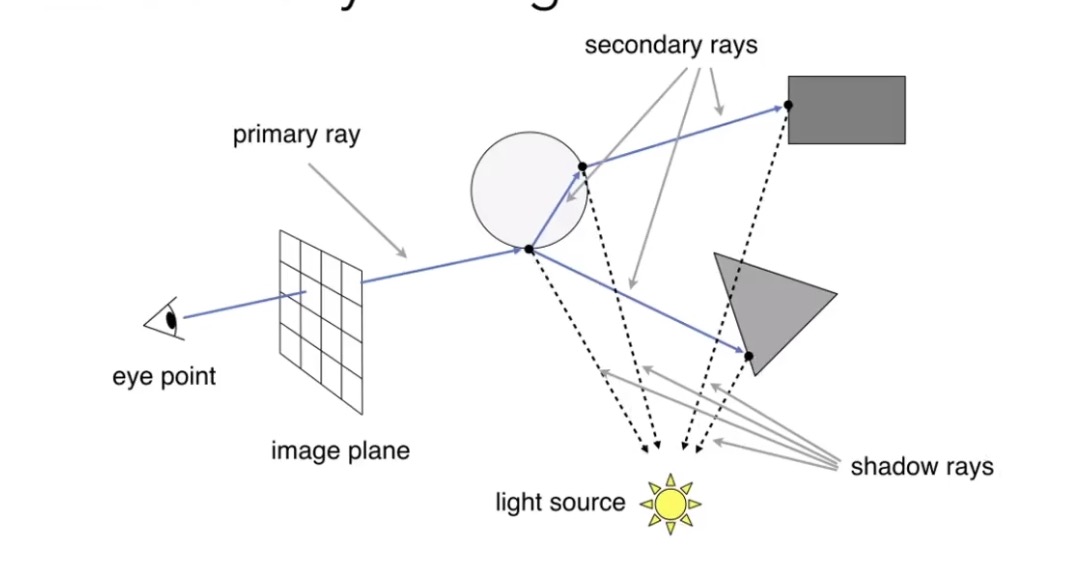
如上图所示,
- primary ray: 最终到达像素的光线。
- secondary ray: 中间所有一系列反射的光线。(我不确定是不是只限定于第二次反射)
- shadow ray: 从光源处发出的所有光线。
step 4 (equation):
- Ray: r(t) = o + td, 0 <= t <= ♾️
任何光线上一点,可以用光线初始强度o + 时间t * 方向d 来表示。
- Sphere: p: (p-c)^2 - R^2 = 0
球上任何一个点p 到球心c 的距离为 R。
- 联立上面两个公式得到:p: (o + td-c)^2 - R^2 = 0
公式之中只有t 是未知量。 直接可以求得。
- Plane Equation: p: (p - p’) . N = 0
通过法线N 和 平面上确定一点p‘ 来确定一个平面。 判断目标点p 到 p’的 向量是否垂直于法线N 来判断p 是否在目标平面上。
- 把plane 和 ray equation 结合起来呢?
我们得知光线上任意一点可以用r(t)来表示。如果这个点在我们的平面上, 也就是r(t)=p。我们可以通过这个等式求得光在什么时间(t)能打到平面上进行折射。联立可以得到:t = (p’ - o) . N / d . N
注意: 我们需要检查一下t是不是非负数。
step 5 (Moller Trumbore Algorithm):
所消耗时间更短。

step 6 (bounding volumes):
如果一束光不与包围盒相交,那么他也不与物品相交。
我们需要尽可能的避免不必要的运算。方法是给每个物体装进一个长方形里面。如果光无法碰触到这个长方形。则我们不需要考虑这个物体余光的碰撞。我们通常设置这种长方形的长宽高沿着xyz轴。
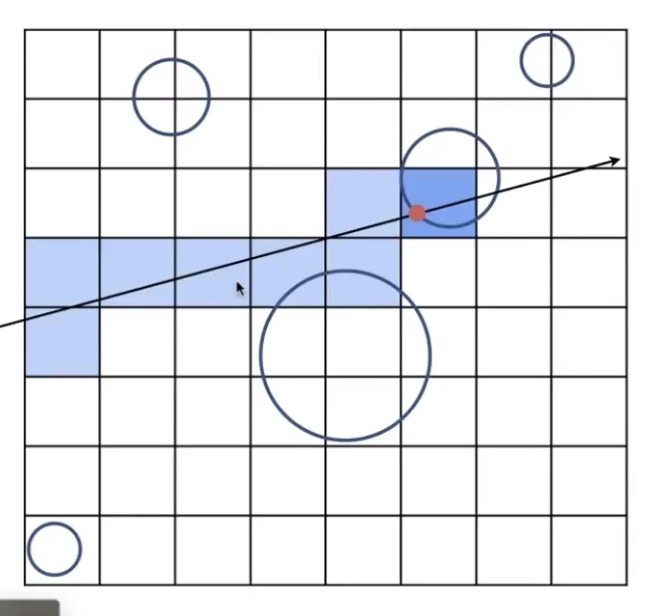
如果光于包围盒相交:
包围盒里面有很多小包围盒。因为计算包围盒与光线是否相交的时间复杂度是高于光与物品相交的。如果光与小包围盒相交。然后进行反射计算。
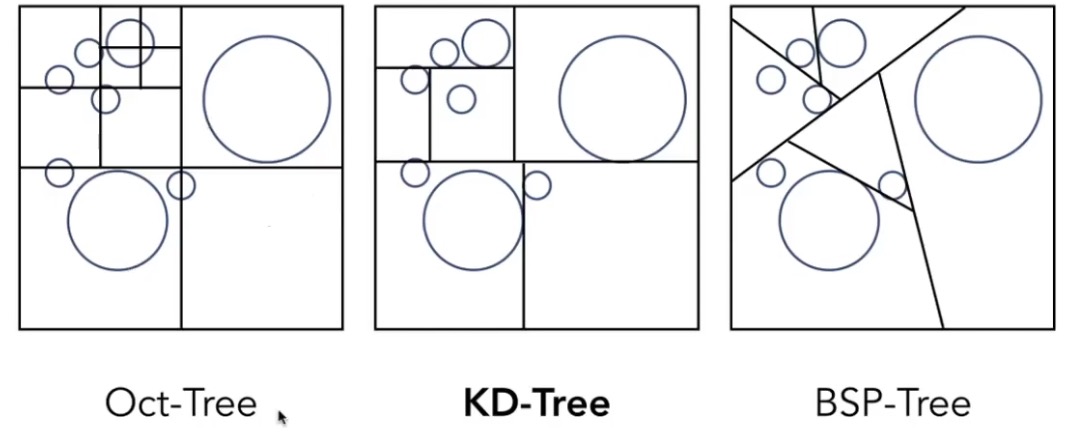
step7 (划分包围盒空间的结构):
Oct-Tree (八叉树): 有不同的分法。比如不停的划分,直到其中有一块包围盒不包含物品位置。
KD-Tree(二叉树): 拼多多树,先横砍一刀沿物品切线。再每个包围盒竖直砍一刀。 目的是保持包围盒的均匀。三纬xyzxyz不断重复切。
BSP-Tree(二叉树): 也是不断砍。但是不好计算。之前我们提到的包围盒AABB就是因为沿着xyz轴的包围盒好被计算。